Признаки подобия треугольников позволяют доказать, что треугольники являются подобными, на основании 2-3 равенств (вместо 6 по определению).
В школьном курсе геометрии, как правило, изучают три признака подобия произвольных треугольников.
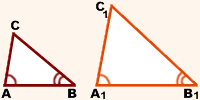
1-й признак подобия треугольников
( подобие треугольников по двум углам)
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
![\[\left. \begin{array}{l} \angle A = \angle {A_1}\\ \angle B = \angle {B_1} \end{array} \right\} \Rightarrow \Delta ABC \sim \Delta {A_1}{B_1}{C_1}\]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-02f9d6c3a19718ed8569d171eaba94ae_l3.png "Rendered by QuickLaTeX.com")
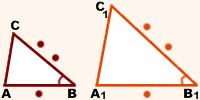
2-й признак подобия треугольников
( подобие треугольников по двум сторонам и углу между ними)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
![\[\left. \begin{array}{l} \frac{{AB}}{{{A_1}{B_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\\ \angle B = \angle {B_1} \end{array} \right\} \Rightarrow \Delta ABC \sim \Delta {A_1}{B_1}{C_1}\]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-95e9474a2a962390578cf3f2a6435f09_l3.png "Rendered by QuickLaTeX.com")
3-й признак подобия треугольников
( подобие треугольников по трём сторонам)
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
![\[\frac{{AB}}{{{A_1}{B_1}}} = \frac{{BC}}{{{B_1}{C_1}}} = \frac{{AC}}{{{A_1}{C_1}}} \Rightarrow \]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-c262ed95e22e7a265d839ca286451f77_l3.png "Rendered by QuickLaTeX.com")
![\[\Delta ABC \sim \Delta {A_1}{B_1}{C_1}\]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-7da6e45ad5db5ee63075435dfd020c07_l3.png "Rendered by QuickLaTeX.com")
Есть еще 4-й признак подобия треугольников —
( подобие треугольников по двум сторонам и наибольшему углу)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а наибольший угол одного равен наибольшему углу другого, то такие треугольники подобны.
Доказав, что треугольники подобны, можно использовать свойства подобных треугольников.
Для доказательства подобия прямоугольных треугольников используют другие признаки. Их мы запишем в следующий раз.
Подобие правильных и подобие равнобедренных треугольников рассмотрим позже.
Признаки подобия треугольников широко используются при решении задач как в курсе планиметрии, так и в курсе стереометрии. Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.