Отрезок, соединяющий середины диагоналей трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции

1) лежит на средней линии трапеции,

2) равен полуразности оснований трапеции.

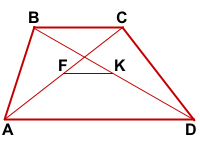Дано: ABCD — трапеция, AD||BC,

F — середина AC, K — середина BD,

MN — средняя линия трапеции

Доказать: FK∈MN,

   

Доказательство:

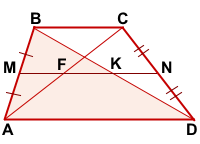Так MN — средняя линия трапеции ABCD, то M — середина AB, N — середина CD, и MN||AD, MN||BC.

Рассмотрим угол ABD.

Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.

Аналогично, для угла BAC:

AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.

Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.

MK — средняя линия треугольника ABD. Поэтому

   

MF — средняя линия треугольника ABC. Поэтому

   

   

Что и требовалось доказать.

Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид

   

Задача.

Основания трапеции равны 10 и 56.

Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

 

   

Ответ:23.