По сторонам треугольника найти его медиану |

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Задача.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

po storonam treugolnika nayti ego medianu Дано: ∆ ABC,

BC=a, AC=b, AB=c,

сторона AC — наибольшая,

BO- медиана.

Найти: BO.

Решение:

po storonam treugolnika nayti medianu

1) На луче BO отложим отрезок OD, OD=BO.

nayti medianu treugolnika po ego storonam

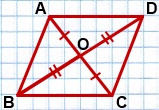
2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

$A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})$

${b^2} + B{D^2} = 2({a^2} + {c^2})$

$B{D^2} = 2({a^2} + {c^2}) - {b^2}$

$BD = \sqrt {2({a^2} + {c^2}) - {b^2}}$

так как BO=1/2 BD (по построению),

$\underline {BO = \frac{1}{2}\sqrt {2({a^2} + {c^2}) - {b^2}} .}$

Если ввести обозначение

$BO = {m_b},$

формула для нахождения медианы треугольника по его сторонам примет вид:

${{m_b} = \frac{1}{2}\sqrt {2({a^2} + {c^2}) - {b^2}} }$

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

${m_a} = \frac{1}{2}\sqrt {2({b^2} + {c^2}) - {a^2}}$

${m_c} = \frac{1}{2}\sqrt {2({a^2} + {b^2}) - {c^2}}$

Приём, который применили для решения задачи — метод удвоения медианы.

One Comment

По сторонам треугольника найти его медиану