Площадь треугольника по координатам |

Как найти площадь треугольника по координатам его вершин?

1способ:

Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.

2 способ:

вывести формулу для нахождения площади и использовать её для вычисления.

Утверждение

Площадь треугольника ABC с вершинами в точках A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) можно вычислить с помощью формулы

$S_{\Delta ABC} = \frac{1}{2}\left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} \right|.$

Доказательство:

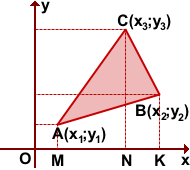ploshchad-treugolnika-po-koordinatam Рассмотрим треугольник ABC,

A(x₁;y₁), B(x₂;y₂), C(x₃;y₃)

Опустим перпендикуляры из вершин треугольника на координатные оси.

$S_{\Delta ABC} = S_{MACN} + S_{NCBK} - S_{MABK}$

$S_{MACN} = \frac{{MA + CN}}{2} \cdot MN = \frac{{y_1 + y_3 }}{2} \cdot (x_3 - x_1 ),$

$S_{NCBK} = \frac{{NC + BK}}{2} \cdot NK = \frac{{y_3 + y_2 }}{2} \cdot (x_2 - x_3 ),$

$S_{MABK} = \frac{{MA + BK}}{2} \cdot MK = \frac{{y_1 + y_2 }}{2} \cdot (x_2 - x_1 ).$

$S_{\Delta ABC} =$

$= \frac{{y_1 + y_3 }}{2} \cdot (x_3 - x_1 ) + \frac{{y_3 + y_2 }}{2} \cdot (x_2 - x_3 ) - \frac{{y_1 + y_2 }}{2} \cdot (x_2 - x_1 ) =$

$= \frac{1}{2}[(y_1 + y_3 )(x_3 - x_1 ) + (y_3 + y_2 )(x_2 - x_3 ) - (y_1 + y_2 )(x_2 - x_1 )] =$

$= \frac{1}{2}[x_3 y_1 - x_1 y_1 \underline { + x_3 y_3 } - x_1 y_3 + x_2 y_3 \underline { - x_3 y_3 } + x_2 y_2 - x_3 y_2 -$

$- x_2 y_1 + x_1 y_1 - x_2 y_2 + x_1 y_2 ] =$

$= \frac{1}{2}[(x_2 y_3 - x_2 y_1 ) + ( - x_1 y_3 + x_1 y_1 ) + (x_1 y_2 - x_1 y_1 ) +$

$+ ( - x_3 y_2 + x_3 y_1 )] =$

$= \frac{1}{2}[x_2 (y_3 - y_1 ) - x_1 (y_3 - y_1 ) + x_1 (y_2 - y_1 ) - x_3 (y_2 - y_1 )] =$

$= \frac{1}{2}[(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )].$

С учетом вариантов взаимного расположения точек A, B и C формула для вычисления площади треугольника по координатам его вершин приобретает вид:

$S_{\Delta ABC} = \frac{1}{2}\left| {(x_2 - x_1 )(y_3 - y_1 ) - (x_3 - x_1 )(y_2 - y_1 )} \right|.$

Что и требовалось доказать.

3 способ:

Найти длины двух сторон и косинус угла между ними и вычислить площадь треугольника через стороны и синус угла между ними.

4 способ:

Найти длину и уравнение одной стороны треугольника и длину высоты, проведённой к этой стороне. Вычислить площадь через сторону и высоту.

Рассмотрим эти способы на конкретном примере.

Найти площадь треугольника, вершины которого имеют координаты A(-1;-3), B(3;4), C(5;-5).

1 способ:

Находим длины сторон треугольника ABC.

$AB = \sqrt {(x_B - x_A )^2 + (y_B - y_A )^2 }$

$AB = \sqrt {(3 - ( - 1))^2 + (4 - ( - 3))^2 } = \sqrt {16 + 49} = \sqrt {65} ;$

$AC = \sqrt {(x_C - x_A )^2 + (y_C - y_A )^2 }$

$AC = \sqrt {(5 - ( - 1))^2 + ( - 5 - ( - 3))^2 } = \sqrt {36 + 4} = \sqrt {40} ;$

$BC = \sqrt {(x_C - x_B )^2 + (y_C - y_B )^2 }$

$BC = \sqrt {(5 - 3)^2 + ( - 5 - 4)^2 } = \sqrt {4 + 81} = \sqrt {85} .$

Поскольку длины сторон выражены иррациональными числами, вычислять площадь треугольника по формуле Герона — не самый лучший способ.

2 способ:

Подставляем в формулу x₁=-1, y₁=-3, x₂=3, y₂=4, x₃=5, y₃=-5:

$S_{\Delta ABC} = \frac{1}{2}\left| {(3 - ( - 1))( - 5 - ( - 3)) - (5 - ( - 1))(4 - ( - 3))} \right| =$

$= \frac{1}{2}\left| {4 \cdot ( - 2) - 6 \cdot 7} \right| = \frac{1}{2} \cdot 50 = 25.$

3 способ:

Угол A образован векторами AC и AB. Отсюда

$\cos \angle A = \frac{{\overrightarrow {AB} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right| \cdot \left| {\overrightarrow {AC} } \right|}}$