Отрезок средней линии трапеции между диагоналями

Утверждение

Отрезок средней линии трапеции, расположенный между её диагоналями, равен полуразности оснований трапеции.

 

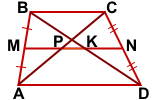Дано:  ABCD — трапеция, AD∥BC,

MN — средняя линия трапеции ABCD,

AC∩MN= P, BD∩MN=K

Доказать:

   

Доказательство:

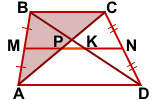1) AM=BM, MP∥BC (так как MN — средняя линия трапеции).

Следовательно, по теореме Фалеса  AP=PC.

Поэтому MP — средняя линия треугольника ABC.

По свойству средней линии треугольника,

   

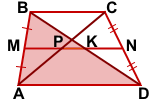2) Аналогично, MK — средняя линия треугольника ABD и

   

   

Что и требовалось доказать.