Выясним, как расположены биссектрисы вертикальных углов.
Утверждение.
Биссектрисы вертикальных углов лежат на одной прямой.
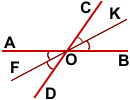 Дано: ∠AOD и ∠СOB — вертикальные,
Дано: ∠AOD и ∠СOB — вертикальные,
OF — биссектриса ∠AOD,
OK — биссектриса ∠СOB.
Доказать: OF и OK лежат на одной прямой.
Доказательство:
1) ∠AOD =∠СOB (как вертикальные).
Так как OF — биссектриса ∠AOD, OK — биссектриса ∠СOB, то
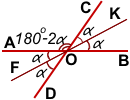 ∠AOF=∠FOD=∠COK=∠KOB=α.
∠AOF=∠FOD=∠COK=∠KOB=α.
2) ∠AOC+∠COB=180° (как смежные).
Отсюда ∠AOC=180°-∠COB=180°-2α.
3) ∠FOK=∠AOF+∠AOC+∠СOB=α+180°-2α+α=180°.
Значит, ∠FOK — развёрнутый. Следовательно, лучи OF и OK лежат на одной прямой.
Что и требовалось доказать.
Таким образом, биссектрисы вертикальных углов являются дополнительными лучами.
Угол между биссектрисами вертикальных углов равен 180°.
