Угол между биссектрисами треугольника

Как найти угол между биссектрисами треугольника?

Задача.

В треугольнике ABC угол C равен α, AD и BE — биссектрисы, пересекающиеся в точке O.

Найти угол AOB.

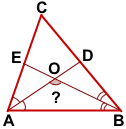ugol-mezhdu-bissektrisami-treugolnika Решение:

1) Так как сумма углов треугольника равна 180°, то в треугольнике ABC

∠BAC+∠ABC+∠C=180°, отсюда

∠BAC+∠ABC=180°-∠C,

∠BAC+∠ABC=180°-α.

2) Так как AD и BE — биссектрисы углов ∠BAC и ∠ABC, то

$\angle BAO = \frac{1}{2}\angle BAC,\angle ABO = \frac{1}{2}\angle ABC,$

$\angle BAO + \angle ABO = \frac{1}{2}\angle BAC + \frac{1}{2}\angle ABC =$

$= \frac{1}{2}(\angle BAC + \angle ABC) = \frac{1}{2}(180^o - \alpha ) = 90^o - \frac{\alpha }{2}.$

3) Для треугольника AOB

∠BAO+∠ABO+∠AOB=180°,

∠AOB=180°-(∠BAO+∠ABO),

$\angle AOB = 180^o - (90^o - \frac{\alpha }{2}) = 90^o + \frac{\alpha }{2}.$

Замечание.

В треугольнике AOB ∠BOD — внешний угол при вершине O. Следовательно,

$\angle BOD = \angle BAO + \angle ABO = 90^o - \frac{\alpha }{2}.$

Вывод:

Один уз углов, образованный при пересечении биссектрис двух углов треугольника, равен сумме 90° и половины третьего угла,

другой — разности 90° и половины третьего угла.

Запоминать для экзамена эти соотношения необязательно. Достаточно самостоятельно провести аналогичные рассуждения.