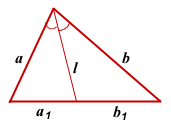
Длина биссектрисы треугольника |

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Утверждение 1

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

najti-dlinu-bissektrisy-treugolnika

$l^2 = ab - a_1 b_1$

$l = \sqrt {ab - a_1 b_1 }$

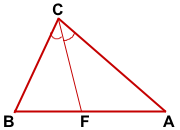dlina-bissektrisy Дано:

ΔABC,

СF — биссектриса ∠ABC

Доказать:

$CF^2 = BC \cdot AC - BF \cdot AF.$

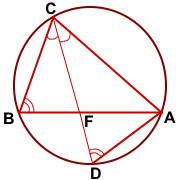dlina-bissektrisy-treugolnika Доказательство:

Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac{{BC}}{{CD}} = \frac{{CF}}{{AC}}, \Rightarrow CD = \frac{{BC \cdot AC}}{{CF}}.$

$FD = CD - CF = \frac{{BC \cdot AC}}{{CF}} - CF.$

По свойству пересекающихся хорд

$BF \cdot AF = CF \cdot FD$

Отсюда

$BF \cdot AF = CF \cdot (\frac{{BC \cdot AC}}{{CF}} - CF)$

$BF \cdot AF = BC \cdot AC - CF^2$

$CF^2 = BC \cdot AC - BF \cdot AF.$

Что и требовалось доказать.

II. Через три стороны треугольника

Утверждение 2

Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

$l_c = \frac{1}{{a + b}}\sqrt {ab(a + b + c)(a + b - c)} .$

Доказательство:

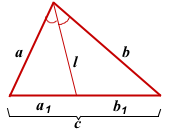dlina-bissektrisy-cherez-storony По свойству биссектрисы треугольника:

$\[ \frac{a}{{a_1 }} = \frac{b}{{b_1 }}, \Rightarrow a_1 b = ab_1 .$

a₁+b₁=c, b₁=c-a₁, поэтому

$a_1 b = a(c - a_1 ),$

$a_1 b = ac - aa_1 ,$

$aa_1 + a_1 b = ac,$

$a_1 (a + b) = ac,$

$a_1 = \frac{{ac}}{{a + b}}.$

Согласно утверждению 1,

$l^2 = ab - a_1 b_1 ,$

$l^2 = ab - a_1 (c - a_1 ) = ab - \frac{{ac}}{{a + b}}(c - \frac{{ac}}{{a + b}}) =$

$= ab - \frac{{ac^2 }}{{a + b}} + \frac{{a^2 c^2 }}{{(a + b)^2 }} = \frac{{ab(a + b)^2 - ac^2 (a + b) + a^2 c^2 }}{{(a + b)^2 }} =$

$= \frac{{ab(a + b)^2 - a^2 c^2 - abc^2 + a^2 c^2 }}{{(a + b)^2 }} = \frac{{ab(a + b)^2 - abc^2 }}{{(a + b)^2 }} =$

$= \frac{{ab}}{{(a + b)^2 }}((a + b)^2 - c^2 ) = \frac{{ab}}{{(a + b)^2 }}((a + b) + c)((a + b) - c) =$

$= \frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c),$

откуда

$l = \sqrt {\frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} ,$

$l_c = \frac{1}{{a + b}}\sqrt {ab(a + b + c)(a + b - c)} .$

Что и требовалось доказать.

Аналогично,

$l_a = \frac{1}{{b + c}}\sqrt {bc(b + c + a)(b + c - a)} ,$

$l_b = \frac{1}{{a + c}}\sqrt {ac(a + c + b)(a + c - b)} .$

III Через две стороны треугольника и угол между ними.

Утверждение 3

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

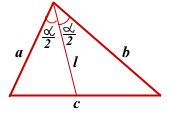
dlina-bissektrisy-cherez-storony-i-ugol

$l_c = \frac{{2ab\cos \frac{\alpha }{2}}}{{a + b}}$

Доказательство:

Найдем площади треугольников BCF, ACF и ABC.

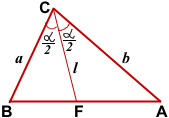
formula-dliny-bissektrisy

$S_{\Delta BCF} = \frac{1}{2}BC \cdot CF \cdot \sin \angle BCF,$

$S_{\Delta ACF} = \frac{1}{2}AC \cdot CF \cdot \sin \angle ACF,$

$S_{\Delta ABC} = \frac{1}{2}AC \cdot BC \cdot \sin \angle BCA.$

Так как

$S_{\Delta ABC} = S_{\Delta BCF} + S_{\Delta ACF} ,$

то

$\frac{1}{2}AC \cdot BC \cdot \sin \angle BCA =$

$= \frac{1}{2}BC \cdot CF \cdot \sin \angle BCF + \frac{1}{2}AC \cdot CF \cdot \sin \angle ACF,$

$ab \cdot \sin \alpha = al \cdot sin\frac{\alpha }{2} + bl \cdot sin\frac{\alpha }{2},$

$ab \cdot \sin \alpha = l \cdot sin\frac{\alpha }{2}(a + b),$

$l = \frac{{ab \cdot \sin \alpha }}{{sin\frac{\alpha }{2}(a + b)}} = \frac{{ab \cdot \sin (2 \cdot \frac{\alpha }{2})}}{{sin\frac{\alpha }{2}(a + b)}} = \frac{{ab \cdot 2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}}}{{sin\frac{\alpha }{2}(a + b)}} = \frac{{2ab\cos \frac{\alpha }{2}}}{{a + b}}.$

Что и требовалось доказать.

Длина биссектрисы треугольника

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики