две биссектрисы равны |

Теорема (Штейнера-Лемуса)

Если в треугольнике две биссектрисы равны, то этот треугольник — равнобедренный.

dve-bissektrisy-ravny Дано:

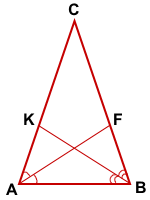
ΔABC,

AF, BK — биссектрисы ΔABC,

AF=BK

Доказать: ΔABC — равнобедренный

Доказательство:

Обозначим BC=a, AC=b, AB=c, BK=l_a, AF=l_b.

Длины биссектрис выражаются формулами

$l_a = \frac{1}{{b + c}}\sqrt {bc(b + c + a)(b + c - a)} ,$

$l_b = \frac{1}{{a + c}}\sqrt {ac(a + c + b)(a + c - b)} .$

По условию l_a=l_b, поэтому

$\frac{1}{{b + c}}\sqrt {bc(b + c + a)(b + c - a)} = \frac{1}{{a + c}}\sqrt {ac(a + c + b)(a + c - b)} ,$

откуда

$\frac{{bc(b + c + a)(b + c - a)}}{{(b + c)^2 }} = \frac{{ac(a + c + b)(a + c - b)}}{{(a + c)^2 }}.$

Разделив обе части равенства на c(a+b+c)≠0 (поскольку a>0, b>0, c>0), получим

$\frac{{b(b + c - a)}}{{(b + c)^2 }} = \frac{{a(a + c - b)}}{{(a + c)^2 }},$

откуда по основному свойству пропорции —

$b(b + c - a)(a + c)^2 = a(a + c - b)(b + c)^2 ,$

$(b^2 + bc - ab)(a^2 + 2ac + c^2 ) = (a^2 + ac - ab)(b^2 + 2bc + c^2 ),$

$a^2 b^2 + 2ab^2 c + b^2 c^2 + a^2 bc + 2abc^2 + bc^3 - a^3 b - 2a^2 bc - abc^2 =$

$= a^2 b^2 + 2a^2 bc + a^2 c^2 + ab^2 c + 2abc^2 + ac^3 - ab^3 - 2ab^2 c - abc^2 ,$

$3ab^2 c + b^2 c^2 - 3a^2 bc + bc^3 - a^3 b - a^2 c^2 - ac^3 + ab^3 = 0,$

$(3ab^2 c - 3a^2 bc) + (b^2 c^2 - a^2 c^2 ) + (bc^3 - ac^3 ) + (ab^3 - a^3 b) = 0,$

$3abc(b - a) + c^2 (b^2 - a^2 ) + c^3 (b - a) + ab(b^2 - a^2 ) = 0,$

$(b - a)(3abc + c^2 (b + a) + c^3 + ab(b + a)) = 0.$

Произведение равно нулю, если хотя бы один из множителей равняется нулю.

$3abc + c^2 (b + a) + c^3 + ab(b + a)) \ne 0$

(так как a, b и c — положительные числа). Значит b-a=0.

Следовательно, a=b. То есть треугольник ABC — равнобедренный.

Что и требовалось доказать.

В 1840 году немецкий математик Дэниэл Лемус написал швейцарскому математику Якобу Штейнеру письмо с просьбой представить геометрическое решение данной задачи.

Доказательство обоих математиков было достаточно сложным. В дальнейшем многие другие математики брались за решение этой задачи. В результате были получены другие варианты доказательства.

Самое простое доказательство теоремы Штейнера-Лемуса — алгебраическое.

Если две биссектрисы треугольника равны

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики