Вычитание векторов |

Разность векторов

Определение

Разность векторов

$\overrightarrow a (a_1 ;a_2 )$

и

$\overrightarrow b (b_1 ;b_2 )$

— это такой вектор

$\overrightarrow c (c_1 ;c_2 ),$

который в сумме с вектором b даёт вектор a:

$\overrightarrow b + \overrightarrow c = \overrightarrow a .$

На основе определения находим координаты вектора

$\overrightarrow c = \overrightarrow a - \overrightarrow b :$

$c_1 = a_1 - b_1 ;c_2 = a_2 - b_2 ,$

то есть

$(\overrightarrow {a_1 ;a_2 } ) - (\overrightarrow {b_1 ;b_2 } ) = (\overrightarrow {c_1 ;c_2 } ).$

Например,

$\overrightarrow a (12; - 5) - \overrightarrow b (7; - 3) = \overrightarrow c (5; - 2).$

Как построить разность двух векторов?

1 способ

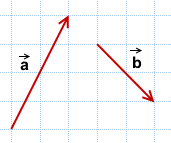raznost-vektorov Из равенства

$\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC}$

следует

$\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {BC} .$

Отсюда получаем

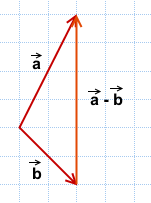
vychitanie-vektorov

правило построения разности двух векторов

Чтобы построить вектор, равный разности векторов

$\overrightarrow a - \overrightarrow b ,$

надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.

Определение

Противоположные векторы — это противоположно направленные векторы одинаковой длины.

Вектор, противоположный вектору

$\overrightarrow a ,$

обозначают

$- \overrightarrow a .$

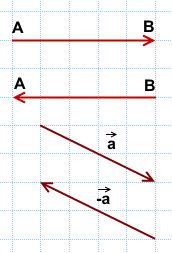protivopolozhnye-vektory Примеры противоположных векторов:

$\overrightarrow {AB} ,\overrightarrow {BA} ;$

$\overrightarrow a ; - \overrightarrow a .$

Свойства противоположных векторов:

1) Противоположные векторы имеют противоположные координаты:

$\overrightarrow {\rm{a}} (a_1 ;a_2 ), - \overrightarrow {\rm{a}} ( - a_1 ; - a_2 ).$

Пусть даны точки

${\rm{A(x}}_{\rm{1}} ;y_1 ),B(x_2 ;y_2 ).$

По определению координат вектора

$\overrightarrow {AB} (x_2 - x_1 ;y_2 - y_1 ),$

$\overrightarrow {BA} (x_1 - x_2 ;y_1 - y_2 ) = ( - (x_2 - x_1 ); - (y_2 - y_1 )).$

2) Сумма противоположных векторов равна нулевому вектору:

$\overrightarrow a + ( - \overrightarrow a ) = \overrightarrow {0.}$

$\overrightarrow a + ( - \overrightarrow a ) = (\overrightarrow {a_1 ;a_2 } ) + (\overrightarrow { - a_1 ; - a_2 } ) = (\overrightarrow {0;0} ) = \overrightarrow {0.}$

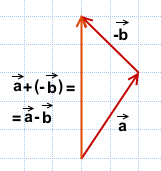
2 способ построения разности векторов

raznost-vektorov Чтобы построить разность векторов

$\overrightarrow a - \overrightarrow b ,$

можно к вектору a прибавить вектор, противоположный вектору b:

$\overrightarrow a - \overrightarrow b = \overrightarrow a + ( - \overrightarrow b ).$

То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.

kak-vychitat-vektory

Добавить комментарий Отменить ответ