В треугольнике ABC на его медиане BM |

В треугольнике ABC на его медиане BM

Задача

В треугольнике ABC на его медиане BM отмечена точка K так, то BK:KM=4:1. Прямая AK пересекает сторону BC в точке P. Найти отношение площади треугольника ABK к площади четырёхугольника KPCM.

Решение:

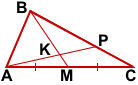v-treugolnike-na-ego-mediane 1)Так как BK:KM=4:1, то BM=5KM. По формуле

$S = \frac{1}{2}a \cdot b \cdot \sin \alpha$

$S_{\Delta ABM} = \frac{1}{2}AM \cdot BM \cdot \sin \angle AMB =$

$= \frac{1}{2}AM \cdot 5KM \cdot \sin \angle AMB =$

$= 5 \cdot (\frac{1}{2}AM \cdot KM \cdot \sin \angle AMB) = 5S_{\Delta AKM} .$

Обозначим S_ΔAKM =x, тогда S_ΔABM =5x, S_ΔABK =S_ΔABM-S_ΔAKM=4x.

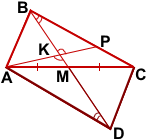v-treugolnike-abc-na-ego-mediane-bm 2) На продолжении луча BM отложим отрезок MD, MD=BM.

Четырёхугольник ABCD — параллелограмм (по признаку).

Поэтому BC∥AD.

3) Рассмотрим треугольники AKD и PKB.

∠AKD=∠PKB (как вертикальные),

∠ADK=∠PBK (как внутренние накрест лежащие при BC∥AD и секущей BD).

Следовательно, треугольники AKD и PKB подобны (по двум углам).

Площади подобных треугольников относятся как квадраты их соответствующих сторон:

$\frac{{S_{\Delta ADK} }}{{S_{\Delta PKB} }} = (\frac{{DK}}{{KB}})^2 = (\frac{6}{4})^2 = \frac{9}{4},$

$S_{\Delta PKB} = \frac{4}{9}S_{\Delta ADK} .$

4) Так как медиана делит треугольник на две равновеликие части, то

${\rm{S}}_{\Delta {\rm{ABM}}} = {\rm{S}}_{\Delta C{\rm{BM}}} = {\rm{S}}_{\Delta {\rm{ADM}}} = 5x.$

Отсюда

${\rm{S}}_{\Delta {\rm{ADK}}} = {\rm{S}}_{\Delta {\rm{ADM}}} + {\rm{S}}_{\Delta {\rm{AKM}}} = 6x,$

${\rm{S}}_{\Delta {\rm{PKB}}} = \frac{4}{9}{\rm{S}}_{\Delta {\rm{ADK}}} = \frac{4}{9} \cdot 6x = \frac{8}{3}x,$

${\rm{S}}_{KPCM} = {\rm{S}}_{\Delta C{\rm{BM}}} - {\rm{S}}_{\Delta {\rm{PKB}}} = 5x - \frac{8}{3}x = \frac{7}{3}x,$

$\frac{{{\rm{S}}_{\Delta {\rm{ABK}}} }}{{{\rm{S}}_{KPCM} }} = \frac{{4x}}{{\frac{7}{3}x}} = \frac{{4 \cdot 3}}{7} = \frac{{12}}{7}.$

Ответ: 12:7.

Добавить комментарий Отменить ответ