В треугольнике ABC известны длины сторон

Задача

В треугольнике ABC известны длины сторон AB=28, AC=56,  точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найти CD.

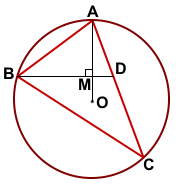Дано:

Δ ABC, AB=28, AC=56,

окр. (O; R) — описанная, BM⊥AO,

BM∩AC=D

Найти: CD

Решение:

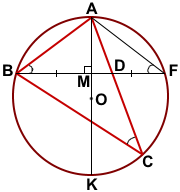1) Продлим AO и BD до пересечения с окружностью в точках K и F.

Так как диаметр AK перпендикулярен хорде BF, то он делит её пополам, то есть точка M — середина BF.

Тогда AM — медиана и высота треугольника ABF, следовательно, треугольник ABF — равнобедренный с основанием BF (по признаку).

Значит, ∠AFB=∠ABF (как углы при основании).

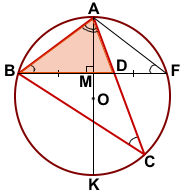∠AFB=∠ACB (как вписанные углы, опирающиеся на одну дугу AB).

Отсюда ∠ABF=∠ACB.

У треугольников ABC и ADB:

1) угол A — общий,

2)∠ABF=∠ACB (по доказанному).

Значит, треугольники ABC и ADB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

   

CD=AC-AD=56-14=42.

Ответ: 42.