В треугольнике биссектриса угла A |

В треугольнике ABC биссектриса угла A делит высоту

Задача

В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найти радиус окружности, описанной около треугольника ABC, если BC=12.

Решение:

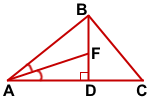v-treugolnike-bissektrisa-delit-vysotu Пусть биссектриса угла A пересекает высоту BD треугольника ABC в точке F.

По условию, BF:FD=5:4.

Рассмотрим треугольник ABD, ∠ADB=90°.

По свойству биссектрисы треугольника,

$\frac{{AB}}{{AD}} = \frac{{BF}}{{FD}} = \frac{5}{4}.$

Пусть k — коэффициент пропорциональности. Тогда AB=5k, AD=4k.

По теореме Пифагора

$AB^2 = AD^2 + BD^2 ,$

$BD = \sqrt {AB^2 - AD^2 } ,$

$BD = \sqrt {(5k)^2 - (4k)^2 } = \sqrt {9k^2 } = 3k.$

По определению синуса

$\sin A = \frac{{BD}}{{AB}},$

$\sin A = \frac{{3k}}{{5k}} = \frac{3}{5}.$

Радиус описанной около треугольника окружности найдём по формуле

$R = \frac{a}{{2\sin \alpha }}.$

Для треугольника ABC формула принимает вид

$R = \frac{{BC}}{{2\sin A}},$

$R = \frac{{12}}{{2 \cdot \frac{3}{5}}} = \frac{{12 \cdot 5}}{{2 \cdot 3}} = 10.$

Ответ: 10.

One Comment

Alex:

02.04.2019 в 13:59

Спасибо. Очень понятно объяснили.

Ответить

Добавить комментарий Отменить ответ