Угол между векторами

Определение

1) Углом между векторами

   

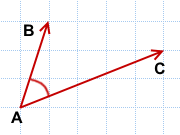
и

   

 

называется угол BAC:

   

2) Углом между двумя ненулевыми векторами называется угол между векторами, равными данным и имеющими общее начало.

Угол между сонаправленными векторами равен 0°.

Поскольку нулевой вектор считается коллинеарным любому вектору, если один из векторов нулевой либо если оба вектора нулевые, то и в этом случае угол между векторами равен 0°.

Угол между равными векторами также равен 0°.

Угол между противоположно направленными векторами равен 180°.

Если угол между векторами равен 90°, то такие векторы называются перпендикулярными.

Рассмотрим понятие угла между векторами на конкретных примерах.

 

Определить угол между векторами:

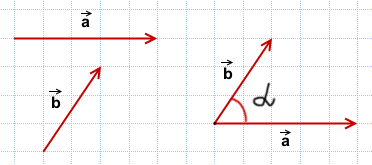
1) Данные векторы не сонаправлены.

Выберем некоторую точку и от неё отложим векторы, равные данным.

 

Угол между ними равен α.

Значит, и угол между данными векторами равен α.

Пишут:

   

 

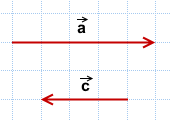
2) Данные векторы противоположно направлены.

Значит, угол между ними равен 180°:

   

Проиллюстрируем этот результат, отложив векторы, равные данным, от одной точки:

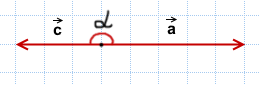
α=180°.

 

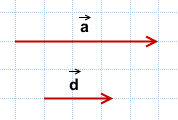3) Поскольку данные векторы сонаправлены, угол между ними равен 0°:

   

 

4)

 

 

 

 

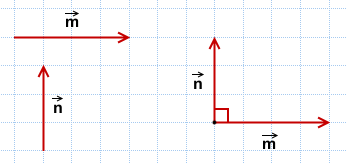
4) Отложим данные векторы от общего начала.

Так как угол между ними равен 90°:

   

векторы перпендикулярны:

   

Угол между векторами можно найти с помощью их скалярного произведения.