Углы в окружности

Рассмотрим углы в окружности и углы, связанные с окружностью.

• Угол с вершиной в центре окружности.
• Угол с вершиной на окружности (его стороны пересекают окружность).
• Угол с вершиной внутри окружности (не в центре).
• Угол с вершиной вне окружности, стороны которого пересекают окружность.

I. Угол с вершиной в центре окружности называется центральным углом.

Стороны центрального угла разбивают окружность на две части. Дугой, соответствующей данному центральному углу, называется та часть, которая содержится внутри угла.

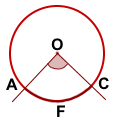Например, центральному углу AOC соответствует дуга AC (или дуга AFC. Обычно дугу называют двумя буквами. Но, поскольку любую из двух, на которые точки A и C делят окружность, можно назвать AC, то третью, дополнительную букву, иногда используют для уточнения выбранной дуги).

Градусная мера дуги окружности равна градусной мере соответствующего центрального угла:

∪AC=∠AOC.

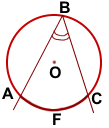II. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Стороны вписанного угла также разбивают окружность на две дуги. Говорят, что вписанный угол опирается на лугу, которая лежит внутри него.

Например, вписанный угол ABC опирается на дугу AC (или дугу AFC).

Вписанный угол равен половине дуги, на которую он опирается:

   

Есть другой вариант формулировки свойства вписанного угла.

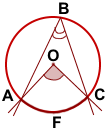Вписанный угол равен половине соответствующего ему центрального угла:

   

 

 

Все вписанные углы, опирающиеся на одну дугу, равны между собой.

 

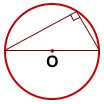Вписанный угол, опирающийся на полуокружность — прямой.

И наоборот: любой прямой вписанный угол опирается на полуокружность.

Другая формулировка этого утверждения:

вписанный угол, опирающийся на диаметр — прямой.

(обратно: Если вписанный угол прямой, то он опирается на диаметр).

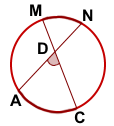
III. Угол, вершина которого лежит в окружности — это угол между пересекающимися хордами.

Угол между пересекающимися хордами равен полусумме дуг, заключённых между  его сторонами и сторонами вертикального ему угла.

 

   

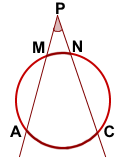
IV. Угол с вершиной вне окружности, обе стороны которого пересекают окружность — это угол между секущими, которые пересекаются вне окружности.

Угол между секущими, пересекающимися вне окружности, измеряется полуразностью большей и меньшей дуг, заключенных между его сторонами.