Точка пересечения медиан |

Как найти точку пересечения медиан треугольника, зная координаты его вершин?

1 способ

Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.

Пример.

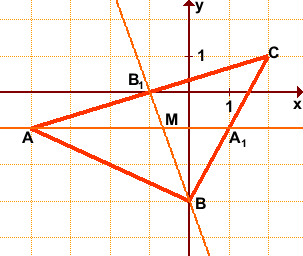
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).

Решение:

Обозначим середины сторон BC и AC через A₁ и B₁ соответственно. По формулам координат середины отрезка

$x_{A_1 } = \frac{{x_B + x_C }}{2} = \frac{{0 + 2}}{2} = 1,$

$y_{A_1 } = \frac{{y_B + y_C }}{2} = \frac{{ - 3 + 1}}{2} = - 1,$

$x_{B_1 } = \frac{{x_A + x_C }}{2} = \frac{{ - 4 + 2}}{2} = - 1,$

$y_{B_1 } = \frac{{y_A + y_C }}{2} = \frac{{ - 1 + 1}}{2} = 0.$

Составим уравнения медиан AA₁ и BB₁.

Уравнение медианы AA₁ можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A₁(1;-1).

$\left\{ \begin{array}{l} - 1 = k \cdot ( - 4) + b, \\ - 1 = k \cdot 1 + b, \\ \end{array} \right. \Rightarrow k = 0,b = - 1,$

то есть уравнение прямой AA₁ y= -1.

B(0;-3), B₁(-1;0). Найдём уравнение медианы BB₁.

$\left\{ \begin{array}{l} - 3 = k \cdot 0 + b, \\ 0 = k \cdot ( - 1) + b, \\ \end{array} \right. \Rightarrow k = - 3,b = - 3,$

откуда уравнение прямой BB₁ y= -3x-3.

Координаты точки пересечения прямых AA₁ и BB₁ ищем как решение системы уравнений

$\left\{ \begin{array}{l} {\rm{y = - 1}}, \\ {\rm{y = - 3x - 3}}{\rm{,}} \\ \end{array} \right. \Rightarrow x = - \frac{2}{3},y = - 1.$

Ответ:

$( - \frac{2}{3}; - 1).$

tochka-peresecheniya-median

2 способ

Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.

Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —

зная координаты A₁(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA₁ в отношении 2:1, считая от точки A.

По формулам деления отрезка в данном отношении

$x = \frac{{nx_1 + mx_2 }}{{m + n}},y = \frac{{ny_1 + my_2 }}{{m + n}}$

$x_M = \frac{{1 \cdot x_A + 2 \cdot x_{A_1 } }}{{2 + 1}} = \frac{{1 \cdot ( - 4) + 2 \cdot 1}}{3} = - \frac{2}{3},$

$y_M = \frac{{1 \cdot y_A + 2 \cdot y_{A_1 } }}{{2 + 1}} = \frac{{1 \cdot ( - 1) + 2 \cdot ( - 1)}}{3} = - 1.$

Точка пересечения медиан треугольника

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики