Теорема Птолемея |

Теорема (Птолемея)

Произведение диагоналей вписанного четырёхугольника равно сумме произведений двух пар его противолежащих сторон.

teorema-ptolemeya Дано:

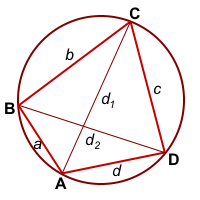
4-угольник ABCD вписан в окр. (O; R)

Доказать:

AC·BD=AB·CD+AD·BC

Доказательство:

I способ

Из треугольников ABC и ADC по теореме косинусов

$AC^2 = AB^2 + BC^2 - 2AB \cdot BC \cdot \cos \angle ABC,$

$AC^2 = CD^2 + AD^2 - 2CD \cdot AD \cdot \cos \angle ADC.$

Введём обозначения AB=a, BC=b, CD=c, AD=d, AC=d₁, BC=d₂.

Тогда

$d_1^2 = a^2 + b^2 - 2ab \cdot \cos \angle ABC,$

$d_1^2 = c^2 + d^2 - 2cd \cdot \cos \angle ADC,$

$\cos \angle ABC = \frac{{a^2 + b^2 - d_1^2 }}{{2ab}},$

$\cos \angle ADC = \frac{{c^2 + d^2 - d_1^2 }}{{2cd}}.$

Так как четырёхугольник ABCD — вписанный, то ∠ABC+∠ADC=180°.

Отсюда cos∠ADC=cos(180°-∠ABC)= -cos∠ABC,

$- \frac{{a^2 + b^2 - d_1^2 }}{{2ab}} = \frac{{c^2 + d^2 - d_1^2 }}{{2cd}},$

$cd(d_1^2 - (a^2 + b^2 )) = ab((c^2 + d^2 ) - d_1^2 ),$

$cd \cdot d_1^2 + ab \cdot d_1^2 = ab(c^2 + d^2 ) + cd(a^2 + b^2 ),$

$d_1^2 = \frac{{ab(c^2 + d^2 ) + cd(a^2 + b^2 )}}{{ab + cd}} =$

$= \frac{{abc^2 + abd^2 + a^2 cd + b^2 cd}}{{ab + cd}} =$

$= \frac{{(abc^2 + a^2 cd) + (abd^2 + b^2 cd)}}{{ab + cd}} =$

$= \frac{{ac(bc + ad) + bd(ad + bc)}}{{ab + cd}} =$

$= \frac{{(ac + bd)(ad + bc)}}{{ab + cd}}.$

Аналогично

$d_2^2 = \frac{{(ab + cd)(ac + bd)}}{{ad + bc}}.$

Отсюда

$d_1^2 \cdot d_2^2 = \frac{{(ac + bd)(ad + bc)(ab + cd)(ac + bd)}}{{(ab + cd)(ad + bc)}} = (ac + bd)^2 ,$

$d_1 \cdot d_2 = ac + bd.$

Что и требовалось доказать.

В ходе доказательства получили полезные соотношения:

1) Диагонали вписанного четырёхугольника связаны с его сторонами равенствами:

$d_1^2 = \frac{{(ac + bd)(ad + bc)}}{{ab + cd}};d_2^2 = \frac{{(ab + cd)(ac + bd)}}{{ad + bc}}.$

2)Отношение диагоналей вписанного четырёхугольника.

$\frac{{d_1^2 }}{{d_2^2 }} = \frac{{(ac + bd)(ad + bc)}}{{ab + cd}}:\frac{{(ab + cd)(ac + bd)}}{{ad + bc}} = \frac{{(ad + bc)^2 }}{{(ab + cd)^2 }},$

$\frac{{d_1 }}{{d_2 }} = \frac{{ad + bc}}{{ab + cd}},$

то есть диагонали вписанного четырехугольника относятся как суммы произведений сторон, сходящихся в концах диагоналей.

II способ

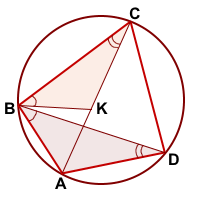teorema-ptolemeya-dokazatelstvo Построим угол CBK, равный углу DBA.

У треугольников CBK и DBA

∠CBK=∠DBA (по построению)

∠BCK=∠BDA (как вписанные углы, опирающиеся на одну дугу AB).

Значит треугольники CBK и DBA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac{{BC}}{{BD}} = \frac{{CK}}{{AD}},$

откуда по основному свойству пропорции

$BC \cdot AD = BD \cdot CK.$

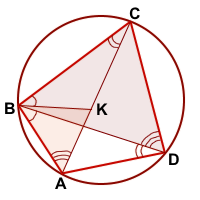teorema-ptolemeya-dokazat Рассмотрим треугольники ABK и DBC.

∠BAK=∠BDC (как вписанные углы, опирающиеся на одну дугу BC).

∠ABK=∠ABD+∠DBK,

∠DBC=∠CBK+∠DBK,

а так как ∠ABD=∠CBK, то и ∠ABK=∠DBC.

Следовательно, треугольники ABK и DBC подобны (по двум углам), и

$\frac{{AB}}{{BD}} = \frac{{AK}}{{CD}},$

$AB \cdot CD = BD \cdot AK.$

Сложим почленно полученные равенства:

$+ \frac{\begin{array}{l} BC \cdot AD = BD \cdot CK \\ AB \cdot CD = BD \cdot AK \\ \end{array}}{{BC \cdot AD + AB \cdot CD = BD \cdot CK + BD \cdot AK}},$

$BC \cdot AD + AB \cdot CD = BD(CK + AK),$

$BC \cdot AD + AB \cdot CD = AC \cdot BD.$

Что и требовалось доказать.

Теорема Птолемея

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики