Сумма квадратов диагоналей |

Сумма квадратов диагоналей параллелограмма

Теорема. (Свойства диагоналей параллелограмма).

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

    \[A{C^2} + B{D^2} = A{B^2} + B{C^2} + C{D^2} + A{D^2}\]

Так как противолежащие стороны параллелограмма равны: AB=CD, AD=BC, то сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон:

    \[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})\]

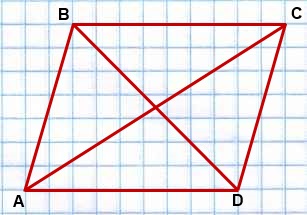
summa kvadratov diagonaley

 

 

Дано:

ABCD — параллелограмм,

AC и BD — диагонали.

 

Доказать:

    \[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})\]

Доказательство:

I споссоб.

summa kvadratov diagonaley parallelogramma

 

1) Опустим перпендикуляры BK и CF на прямую, содержащую сторону AD.

2) Рассмотрим прямоугольный треугольник BDK.

По теореме Пифагора

    \[B{D^2} = B{K^2} + K{D^2}.\]

3) Аналогично, из прямоугольного треугольника ACF

    \[{A{C^2} = C{F^2} + A{F^2}}\]

4) Сложим почленно полученные равенства:

    \[\begin{array}{l} B{D^2} = B{K^2} + K{D^2}\\ \underline {A{C^2} = C{F^2} + A{F^2}} \\ A{C^2} + B{D^2} = B{K^2} + C{F^2} + K{D^2} + A{F^2} \end{array}\]

BK=CF (как высоты параллелограмма, проведенные к одной стороне), поэтому

    \[A{C^2} + B{D^2} = 2B{K^2} + K{D^2} + A{F^2}\]

5) Из прямоугольного треугольника ABK по теореме Пифагора

    \[B{K^2} = A{B^2} - A{K^2}.\]

6) KD=AD-AK, AF=AD+FD, поэтому

    \[A{C^2} + B{D^2} = \]

    \[ = 2(A{B^2} - A{K^2}) + {(AD - AK)^2} + {(AD + FD)^2}\]

7) BK=CF, AB=CD. Значит, прямоугольные треугольники ABK и DCF равны (по катету и гипотенузе).

Следовательно, их соответствующие стороны равны: AK=DF. Отсюда,

    \[A{C^2} + B{D^2} = \]

    \[ = 2(A{B^2} - A{K^2}) + {(AD - AK)^2} + {(AD + AK)^2}\]

Раскрываем скобки:

    \[A{C^2} + B{D^2} = 2A{B^2}\underline { - 2A{K^2}} + \]

    \[ + A{D^2}\underline{\underline { - 2 \cdot AD \cdot AK}} + \underline {A{K^2}} + \]

    \[ + A{D^2}\underline{\underline { + 2 \cdot AD \cdot AK}} + \underline {A{K^2}} \]

Упрощаем

    \[A{C^2} + B{D^2} = 2A{B^2} + 2A{D^2}\]

    \[A{C^2} + B{D^2} = 2{(A{B^2} + AD^2}).\]

Что и требовалось доказать.

II способ.

Свойство диагоналей параллелограмма можно рассматривать как следствие из теоремы косинусов.

Этот способ доказательства будет рассмотрен в следующий раз.

2 Comments

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *