Средняя линия треугольника на клетчатой бумаге |

Рассмотрим, как может быть найдена средняя линия треугольника по рисунку на клетчатой бумаге.

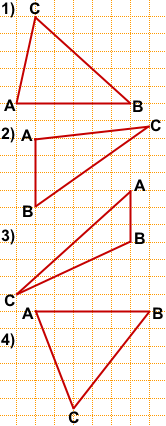
Задача 1

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

Решение:

Как правило, в таких заданиях на чертеже треугольник расположен таким образом, что по клеточкам посчитать длину средней линии невозможно.

Но задача легко разрешима с применением свойства средней линии треугольника:

средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна её половине.

Следовательно, чтобы найти длину средней линии, параллельной стороне AB, надо найти длину отрезка AB.

Длина искомой средней линии равна её половине.

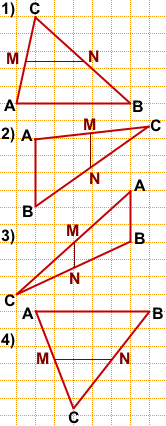
srednyaya-liniya-treugolnika-na-bumage

1) AB=6,

$MN = \frac{1}{2}AB = \frac{1}{2} \cdot 6 = 3;$

$2)MN = \frac{1}{2}AB = \frac{1}{2} \cdot 4 = 2;$

$3)MN = \frac{1}{2}AB = \frac{1}{2} \cdot 3 = 1,5;$

$4)MN = \frac{1}{2}AB = \frac{1}{2} \cdot 6 = 3.$

А как быть, если длину стороны треугольника посчитать по клеточкам не получается?

Возможно, в этом случае сторону треугольника можно найти с помощью теоремы Пифагора.

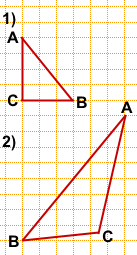
najti-srednyuyu-liniyu-treugolnika-po-kletochkam

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.

Найдите длину его средней линии, параллельной стороне AB.

Решение:

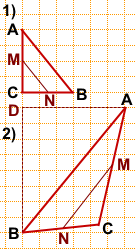srednyaya-liniya-na-kletochnoj-bumage 1)В прямоугольном треугольнике ABC AB — гипотенуза.

AC=4, BC=3.

По теореме Пифагора

$AB^2 = AC^2 + BC^2 ,$

$AB = \sqrt {4^2 + 3^2 } = 5.$

Средняя линия MN равна половине гипотенузы:

$MN = \frac{1}{2}AB = \frac{1}{2} \cdot 5 = 2,5.$

2)Достроим по клеточкам прямоугольный треугольник ABD с гипотенузой AB.

По теореме Пифагора

$AB^2 = AD^2 + BD^2 ,$

$AB = \sqrt {6^2 + 8^2 } = 10,$

$MN = \frac{1}{2}AB = \frac{1}{2} \cdot 10 = 5.$

Средняя линия треугольника на клетчатой бумаге