Следствие теоремы синусов

Отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной около этого треугольника окружности:

$\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \gamma }} = 2R$

sledstvie teoremyi sinusov

Дано: ∆ ABC,

окружность (O, R) — описанная,

BC=a, ∠A=α.

Доказать:

$\frac{a}{{\sin \alpha }} = 2R$

Доказательство:

sledstvie iz teoremyi sinusov I. Если треугольник ABC — остроугольный.

Проведем из точки B диаметр BD.

∠D=∠A=α (как вписанные углы, опирающиеся на одну хорду BC).

∠BCD=90º (как вписанный угол, опирающийся на диаметр).

Из прямоугольного треугольника BCD по определению синуса острого угла прямоугольного треугольника

$\sin \angle BDC = \frac{{BC}}{{BD}},$

BD=2R,

$\sin \alpha = \frac{a}{{2R}},$

$\Rightarrow \frac{a}{{\sin \alpha }} = 2R.$

Что и требовалось доказать.

I. Если треугольник ABC — тупоугольный.

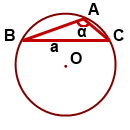
sledstvie iz teoremyi sinusov formula

В этом случае четырехугольник ABCD — вписанный в окружность, а значит, сумма его противолежащих углов равна 180º:

∠A+∠D=180º.

Отсюда ∠D=∠A=180º — α.

Так как

$\sin ({180^o} - \alpha ) = \sin \alpha ,$

дальнейшее решение совпадает с решением I.

III. Если треугольник ABC — прямоугольный.

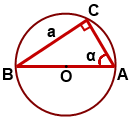
sledstvie iz teoremyi sinusov dlya R

∠C=90º, AB — диаметр, AB=2R.

По определению синуса

$\sin \angle A = \frac{{BC}}{{AB}},$

$\sin \alpha = \frac{a}{{2R}}, \Rightarrow$

$\frac{a}{{\sin \alpha }} = 2R.$

$\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \gamma }},$

то

$\underline {\frac{a}{{\sin \alpha }} = \frac{b}{{\sin \beta }} = \frac{c}{{\sin \gamma }} = 2R.}$