Определение 1
Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
![]()
где
![]()
(0°≤φ≤180°).
Если хотя бы один из векторов нулевой, то скалярное произведение принимают равным нулю.
Определение 2
Скалярным произведением двух векторов
![]()
называется сумма произведений их соответствующих координат:
![]()
(В учебнике в качестве определения даётся одно, другое доказывается как теорема).
Свойства скалярного произведения:
![]()
(переместительное);
![]()
(сочетательное);
![]()
(распределительное);
![]()
— такое произведение называется скалярным квадратом вектора a.
Из определения следует формула для нахождения угла между ненулевыми векторами:
![Rendered by QuickLaTeX.com \[ \cos \varphi = \frac{{\overrightarrow a \cdot \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}. \]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-c4425a4b364228bc25edeb5692658799_l3.png)
Поскольку модуль ненулевого вектора — положительное число, то знаменатель этой дроби — положительное число. Значит знак дроби зависит от знака числителя, то есть от знака скалярного произведения векторов.
Таким образом, знак косинуса угла между векторами совпадает со знаком скалярного произведения векторов.
Поскольку косинус острого угла равен положительному числу, косинус тупого угла равен отрицательному числу, а косинус 90° равен нулю, то
![]()
![]()
3)Свойство перпендикулярных векторов и признак перпендикулярности векторов:
![]()
то есть
![]()
Рассмотрим применение скалярного произведения на практике.
№ 1. Найти скалярное произведение векторов
![]()
![]()
Решение:
![]()
подставляем данные из условия и значение cos120°:
![]()
![]()
Подставляем координаты векторов:
![]()
№ 2. Дано:
![]()
Найти:
![]()
![]()
![]()
Решение:
Подставляем данные условия и cos60°
![]()
![]()
![]()
![]()
![]()
№ 3. Даны векторы
![]()
При каком значении x эти векторы перпендикулярны?
Решение:
Векторы перпендикулярны, если их скалярное произведение равно нулю. Найдём скалярное произведение данных векторов и выясним, при каком значении переменной x оно равно нулю.
![]()
![]()
![]()
Ответ: -6 или 6.
№ 4. Найти косинус угла между векторами
![]()
и
![]()
если
![]()
![]()
Решение:
![Rendered by QuickLaTeX.com \[\cos \angle (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a \cdot \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}.\]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-d884f2857b10283c2d41af00b0c899f8_l3.png)
По свойствам скалярного произведения
![]()
![]()
![]()
Следовательно,
![]()
![]()
![]()
Построим векторы
![]()
используя правило треугольника:
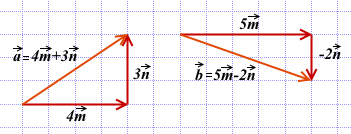
Длины векторов можем найти по теореме Пифагора:
![]()
![]()
Итак,
![]()
Ответ:
![]()
