Задача 1
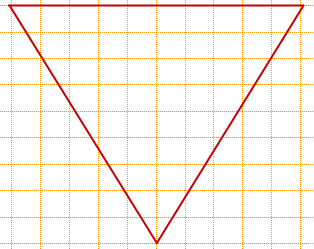 На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус вписанной в него окружности.
Решение:
Поскольку формула радиуса вписанной в правильный треугольник окружности содержит иррациональность:
![]()
использовать её на экзамене, где требуется точный ответ, а не его приближённое значение, нет смысла. Да и длина стороны треугольника задана в таких заданиях не целым числом.
Зато высота треугольника — целое число. По свойству равностороннего треугольника его высота равна сумме радиусов вписанной и описанной окружности:
![]()
причем
![]()
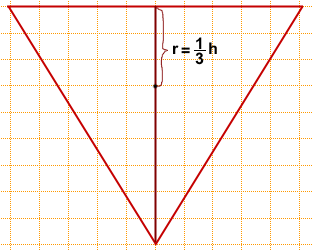 Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.
Итак, чтобы найти радиус вписанной в равносторонний треугольник окружности, нужно посчитать по клеткам длину высоты и найти от неё треть.
В данной задаче длина высоты равна 9 клеткам (h=9), следовательно,
![]()
Ответ: 3.
Задача 2
На клетчатой бумаге с размером клетки 1×1 изображён равносторонний треугольник. Найти радиус описанной около него окружности.
Решение:
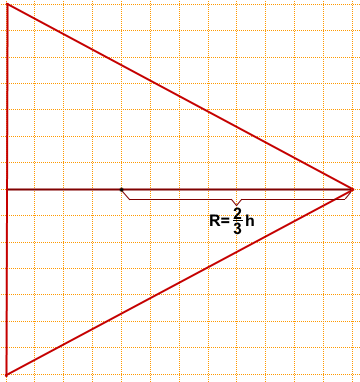 Находим по клеткам высоту данного треугольника:
Находим по клеткам высоту данного треугольника:
h=12.
Радиус описанной около равностороннего треугольника окружности составляет две третьих его высоты:
![]()
![]()
Ответ: 8.
