Равенство равнобедренных треугольников

Равенство равнобедренных треугольников можно доказать, используя признаки равенства произвольных треугольников.

Признаки равенства равнобедренных треугольников

1) (По основанию и боковой стороне)

Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедренного треугольника, то такие треугольники равны.

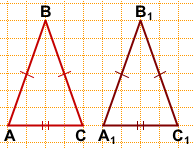Дано: ΔABC, AB=BC,

ΔA₁B₁C₁, A₁B₁=B₁C₁,

AB=A₁B₁, AC=A₁C₁.

Доказать: ΔABC=ΔA₁B₁C₁.

Доказательство:

В треугольниках ABC и A₁B₁C₁:

1) AB=A₁B₁ (по условию);

2) AC=A₁C₁ (по условию).

2) Так как AB=BC, A₁B₁=B₁C₁, AB=A₁B₁, то BC=B₁C₁.

Следовательно, ΔABC=ΔA₁B₁C₁ (по трём сторонам).

Что и требовалось доказать.

 

2) (По боковой стороне и углу при вершине)

Если боковая сторона и угол при вершине одного равнобедренного треугольника соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.

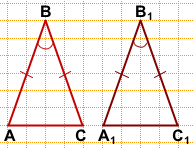
Дано: ΔABC, AB=BC,

ΔA₁B₁C₁, A₁B₁=B₁C₁,

AB=A₁B₁,∠B=∠B₁.

Доказать: ΔABC=ΔA₁B₁C₁.

Доказательство:

В треугольниках ABC и A₁B₁C₁:

1) AB=A₁B₁ (по условию);

3) ∠B=∠B₁ (по условию);

2) Так как AB=BC, A₁B₁=B₁C₁, AB=A₁B₁, то BC=B₁C₁.

Следовательно, ΔABC=ΔA₁B₁C₁ (по двум сторонам и углу между ними).

Что и требовалось доказать.

 

3) (По основанию и углу при основании)

Если основание и угол при основании одного равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.

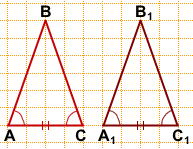
Дано: ΔABC, AB=BC,

ΔA₁B₁C₁, A₁B₁=B₁C₁,

AC=A₁C₁, ∠A=∠A₁

Доказать: ΔABC=ΔA₁B₁C₁.

Доказательство:

В треугольниках ABC и A₁B₁C₁:

1) AC=A₁C₁ (по условию);

2) ∠A=∠A₁ (по условию);

3) ∠C=∠A, ∠C₁ =∠A₁ (как углы при основании равнобедренного треугольника). Значит ∠C=∠C₁.

Следовательно, ΔABC=ΔA₁B₁C₁ (по стороне и двум прилежащим к ней углам).

Что и требовалось доказать.