От точки пересечения диагоналей трапеции |

Задача

В равнобедренную трапецию, периметр которой 220, а площадь равна 2420, можно вписать окружность.

Найти расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

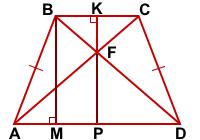ot-tochki-peresecheniya-diagonalej-trapecii Дано: ABCD — трапеция,

AD || BC, AB=CD,

P_ABCD=220, S_ABCD=2420,

AC∩BC=F, FK⊥BC

Найти: FK

Решение:

Так как AB=CD, то AD+BC=2AB.

P_ABCD=AD+BC+AB+CD=4AB=2(AD+BC)=220.

Следовательно, AB=55, AD+BC=110.

Проведём через точки B и F высоты KP и BM.

$S_{ABCD} = \frac{{AD + BC}}{2} \cdot KP,$

$KP = \frac{{2S_{ABCD} }}{{AD + BC}} = \frac{{2 \cdot 2420}}{{110}} = 44 = BM.$

Из прямоугольного треугольника ABM по теореме Пифагора

$AB^2 = AM^2 + BM^2 ,$

$AM = \sqrt {AB^2 - BM^2 } = \sqrt {55^2 - 44^2 } = 33.$

По свойству равнобедренной трапеции,

$AM = \frac{{AD - BC}}{2}, \Rightarrow AD - BC = 2AM = 2 \cdot 33 = 66.$

$+ \frac{\begin{array}{l} AD + BC = 110 \\ AD - BC = 66 \\ \end{array}}{{2AD = 176,}}$

$AD = 88,BC = 22.$

Рассмотрим треугольники AFD и CFB.

∠DAF=∠BCF (как внутренние односторонние при AD || BC и секущей AC),

∠FAD=∠FCB (как смежные).

Следовательно, треугольники AFD и CFB подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих элементов:

$\frac{{AD}}{{BC}} = \frac{{FP}}{{FK}}$

Пусть FK=x, тогда FP=44-x,

$\frac{{88}}{{22}} = \frac{{44 - x}}{x} \Rightarrow x = 8,8.$

Ответ: 8,8.

Расстояние от точки пересечения диагоналей трапеции