Радиус вписанной в прямоугольный |

Утверждение.

Радиус вписанной в прямоугольный треугольник окружности равен

$r = \frac{{a + b - c}}{2},$

где a и b — катеты, c — гипотенуза.

Доказательство:

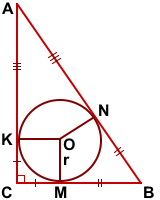radius-vpisannoj-v-pryamougolnyj-treugolnik-okruzhnosti Пусть в прямоугольном треугольнике ABC катеты BC=a, AC=b, гипотенуза AB=c.

Проведём радиусы OK, OM, ON к сторонам треугольника.

$OK \bot AC,OM \bot BC,ON \bot AB$

$AK = AN,BM = BN,CK = CM$

(как отрезки касательных, проведённых из одной точки).

Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.

Следовательно,

$a + b = BC + AC = BM + CM + AK + CK =$

$= BN + CM + AN + CK = (BN + AN) + CM + CK =$

$= c + 2r,$

то есть

$a + b = c + 2r, \Rightarrow 2r = a + b - c,$

Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности

$r = \frac{{a + b - c}}{2}$

Что и требовалось доказать.

One Comment

Спасибо огромное, очень помогли

Радиус вписанной в прямоугольный треугольник окружности