Поворот

Отметим на плоскости точку O — центр поворота. Зададим угол α — угол поворота.

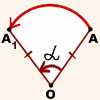
Определение

Поворот плоскости вокруг точки O на угол α — это отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, что

   

   

При этом точка O остаётся на месте (отображается сама в себя), а все остальные точки поворачиваются вокруг точки O в одном и том же направлении — либо по часовой стрелке, либо против часовой стрелки.

Утверждение

Поворот является движением

(то есть отображением плоскости на себя, сохраняющим расстояние).

Доказательство:

Если точки A, O и B не лежат на одной прямой.

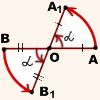
Пусть точка O — центр поворота, α — угол поворота. При повороте вокруг точки O на угол α против часовой стрелки точка A отобразится в точку A1, точка B — в точку B1.

Проведём отрезки AB и A1B1.

Рассмотрим треугольники AOB и A1OB1.

1) OA=OA1;

2) OB=OB1 (по определению поворота).

   

   

Следовательно, треугольники AOB и A1OB1 равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1.

Если точки A, O и B лежат на одной прямой.

   

При повороте в направлении по часовой стрелке все рассуждения аналогичны.

Равенство A1B1=AB означает, что при повороте расстояние между точками сохраняется, а значит, поворот является движением.

Что и требовалось доказать.