Площадь треугольника, изображённого на клетчатой бумаге

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

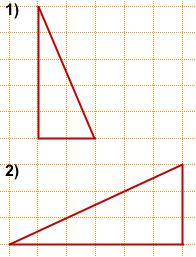На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

 

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

   

где a и b — катеты.

Длину катетов считаем по клеточкам.

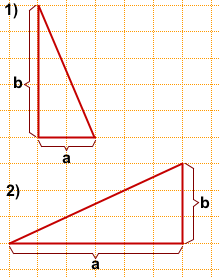1) a=2, b=5,

   

2) a=6, b=3,

   

 

 

Задача 2

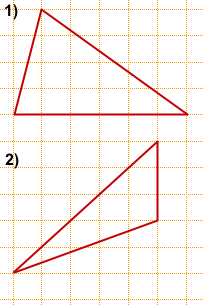На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

 

Решение:

 

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

   

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

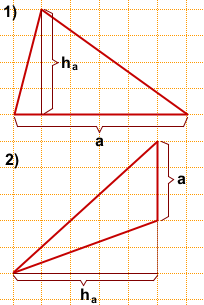a  и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

1) a=6, h_a=4,

   

2) a=3, h_a=5,

   

 

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

Задача 3

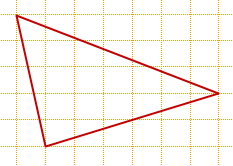
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

 

 

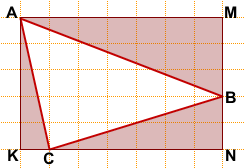
Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

   

Площадь прямоугольника найдём по формуле S=ab.

   

Площади прямоугольных треугольников найдём по формуле

   

где a и b — катеты.

   

   

   

Отсюда