Первый признак подобия треугольников

Теорема

(Первый признак подобия треугольников — подобие треугольников по двум углам)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

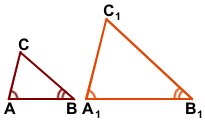Дано: ΔABC, ΔA₁B₁C₁,

∠A=∠A₁, ∠B=∠B₁,

Доказать: ΔABC∼ ΔA₁B₁C₁

Доказательство:

1) По теореме о сумме углов треугольника

∠C=180°-(∠A+∠B), ∠C₁=180°-(∠A₁+∠B₁).

Так как ∠A=∠A₁ и ∠B=∠B₁, то и ∠C=∠C₁.

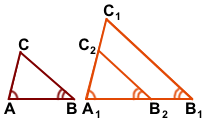2) На луче A₁B₁ отложим отрезок A₁B₂, A₁B₂=AB.

3) Через точку B₂ проведем прямую B₂C₂, параллельную прямой B₁C₁.

4) ∠A₁B₂C₂=∠A₁B₁C₁ (как соответственные при B₂C₂ ∥ B₁C₁ и секущей A₁B₁).

Значит, ∠A₁B₂C₂=∠B.

5) В треугольниках A₁B₂C₂ и ABC:

• ∠A₁ =∠A,
• ∠A₁B₂C₂=∠B,
• A₁B₂ =AB.

Значит, ΔA₁B₂C₂ = ΔABC (по стороне и двум прилежащим к ней углам).

Из равенства треугольников следует равенство соответствующих сторон: A₁C₂=AC.

6) По теореме о пропорциональных отрезках,

   

Так как A₁B₂ =AB и A₁C₂=AC, то

   

7) Аналогично доказывается, что

   

8) Таким образом, в треугольниках ABC и A₁B₁C₁:

∠A=∠A₁, ∠B=∠B₁, ∠C=∠C₁,

   

Значит, ΔABC∼ ΔA₁B₁C₁ (по определению подобных треугольников).

Что и требовалось доказать.

При решении задач чаще других используется именно 1-й признак подобия треугольников.