Теорема (свойство вписанного четырёхугольника)
Сумма противолежащих углов вписанного четырёхугольника равна 180°.
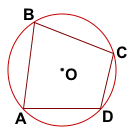 Дано: ABCD вписан в окр. (O; R)
Дано: ABCD вписан в окр. (O; R)
Доказать:
∠A+∠C=180°,
∠B+∠D=180°.
Доказательство:
∠A — вписанный угол, опирающийся на дугу BCD.
∠C — вписанный угол, опирающийся на дугу DAB.
Так как вписанный угол равен половине дуги, на которую он опирается, то
![]()
![]()
Отсюда
![]()
![]()
Аналогично,
![]()
Что и требовалось доказать.
Теорема (признак вписанного четырёхугольника)
Около четырёхугольника можно описать окружность, если сумма его противолежащих углов равна 180°.
Дано: ABCD — четырёхугольник,
∠B+∠D=180°
Доказать: ABCD можно вписать в окружность
Доказательство:
Опишем окружность около треугольника ABC и докажем, что точка D лежит на этой окружности.
Доказательство будем вести методом от противного.
Предположим, что точка D не лежит на описанной около треугольника ABD окружности. Тогда D лежит либо внутри этой окружности, либо вне её.
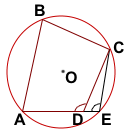 Пусть точка D лежит внутри окружности и луч AD пересекает окружность в точке E.
Пусть точка D лежит внутри окружности и луч AD пересекает окружность в точке E.
В этом случае четырёхугольник ABCE — вписанный, и сумма его противолежащих углов равна 180°: ∠B+∠E=180°.
По условию, ∠B+∠D=180°. Отсюда следует, что ∠D=∠E.
Но угол D — внешний угол треугольника DCE при вершине D.
Так как внешний угол треугольника равен сумме двух внутренних не смежных с ним углов, то
∠ADC=∠DEC+∠DCE, то есть угол D не может быть равным углу E. Пришли к противоречию. А значит, точка D не может лежать внутри окружности, описанной около треугольника ABC.
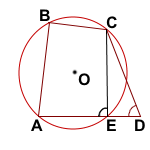 Предположим, что точка D лежит вне описанной около треугольника ABC окружности.
Предположим, что точка D лежит вне описанной около треугольника ABC окружности.
Луч AD пересекает окружность в точке E.
Тогда ABCE — вписанный четырёхугольник и ∠B+∠E=180°.
По условию, ∠B+∠D=180°. Получаем, что ∠D=∠E.
Но угол E — внешний угол треугольника ECD при вершине E. А значит,
∠AEC=∠EDC+∠DCE, то есть углы D и E не могут быть равными. Противоречие получили потому, что предположили, что точка D лежит вне окружности.
Так как точка D не может лежать внутри либо вне описанной около треугольника ABC окружности, то D лежит на этой окружности. Это значит, что около четырёхугольника ABCD можно описать окружность.
Что и требовалось доказать.
На основании свойства и признака вписанного четырёхугольника сформулируем необходимое и достаточное условие вписанного четырёхугольника.
Теорема (Необходимое и достаточное условие вписанного четырёхугольника)
Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма его противолежащих углов равна 180°.

А как же параллелограмм? Необходимое НО недостаточное условие вписанного четырёхугольника
Из параллелограммов описать окружность можно только около прямоугольника и квадрата. Для них признак вписанного четырёхугольника выполнен.