На стороне треугольника как на диаметре построена окружность

Задача

На стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.

Найти AH.

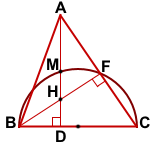Дано: ΔABC,

AD=49, AD и BF — высоты, AD ∩ BF=H,

полуокружность с диаметром BC пересекает AD в точке M, MD=42

Найти: AH

Решение:

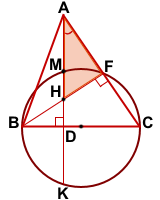Достроим полуокружность до окружности и продлим AD до пересечения с окружностью в точке K.

Точка F лежит на окружности ( если вписанный угол — прямой, то он опирается на диаметр).

Прямоугольные треугольники ADC и AFH подобны по общему острому углу A.

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

отсюда

   

По свойству секущих, проведённых из одной точки,

   

AM=AD-MD=49-42=7,

DK=MD=42 (так как диаметр BC перпендикулярен хорде MK, то он проходит через её середину).

AK=AD+DK=49+42=91.

Следовательно,

   

Ответ: 13.