Медиана делит треугольник

Утверждение.

Медиана делит треугольник на два равновеликих треугольника.

Равновеликие треугольники — это треугольники, имеющие равные площади.

То есть медиана делит исходный треугольник на два треугольника с равными площадями (или медиана делит площадь треугольника пополам).

mediana-delit-treugolnik Дано: ABC,

BM — медиана.

Доказать:

${S_{\Delta ABM}} = {S_{\Delta CBM}}$

Доказательство:

1 способ:

$S = \frac{1}{2}ab\sin \alpha$

${S_{\Delta ABM}} = \frac{1}{2} \cdot AM \cdot BM \cdot \sin \angle AMB,$

${S_{\Delta CBM}} = \frac{1}{2} \cdot CM \cdot BM \cdot \sin \angle CMB.$

mediana-delit-treugolnik-na-dva ∠AMB +∠CMB=180º (как смежные).

sin∠CMB=sin(180º-∠AMB)=sin∠AMB.

Следовательно,

${S_{\Delta CBM}} = \frac{1}{2} \cdot CM \cdot BM \cdot \sin \angle CMB =$

$= \frac{1}{2} \cdot AM \cdot BM \cdot \sin \angle AMB = {S_{\Delta ABM}}$

Что и требовалось доказать.

2 способ:

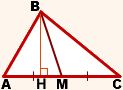mediana-delit-ploshchad-treugolnika Проведём высоту BH.

$S = \frac{1}{2}a \cdot h_a$

$S_{\Delta ABM} = \frac{1}{2}AM \cdot BH,$

$S_{\Delta CBM} = \frac{1}{2}CM \cdot BH.$

Так как AM=CM, то

$S_{\Delta ABM} = S_{\Delta CBM} .$

Что и требовалось доказать.

2 Comments

а можно попроще? без син, мы их не изучали

admin:

19.05.2019 в 22:10

Alex, утверждение доказано двумя способами.

Ответить

2 Comments