Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой.  90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

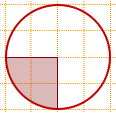
1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Решение:

Так как центральный угол, соответствующий данному сектору, равен 90º, то

S_{сектора}=S_круга:4=60:4=15.

Обратная задача.

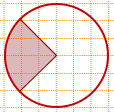2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Решение:

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

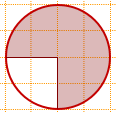3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Решение:

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

S_круга=S_{сектора}:(3/4)=21: (3/4)=21·4:3=28.

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Решение:

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

S_круга=S_{сектора}:(1/8)=11: (1/8)=11·8=88.

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Решение:

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{незакрашенного сектора}=S_круга:8=96:8=12.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

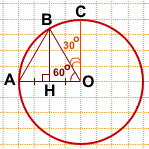Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

∠BOC=∠AOC-∠AOB=90°-60°=30°.

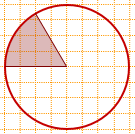6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Решение:

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

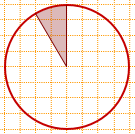7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Решение:

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

S_круга=S_{сектора}:(1/12)=24: (1/12)=24·12=288.

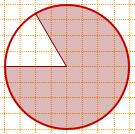8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Решение:

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

S_круга=S_{сектора}:(5/6)=60: (5/6)=60·6:5=72°.

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) 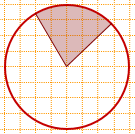Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

S_{сектора}=S_круга·(5/24)=S_круга:24·5,

S_круга=S_{сектора}:(5/24)=S_круга: 5·24.

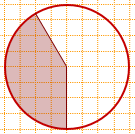10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

S_{сектора}=S_круга·(5/12),

S_круга=S_{сектора}:(5/12).

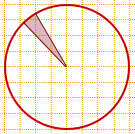11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

и т.д.

 

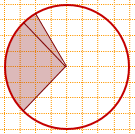12) Центральный угол равен 15+90=105°

(либо 180-30-45=105°),

площадь заштрихованного сектора составляет

1/24+1/4=7/24 и т.д.