Косинус острого угла в прямоугольном треугольнике

Что такое косинус в треугольнике?

Как найти косинус острого угла в прямоугольном треугольнике?

Определение

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

kosinus v treugolnike Например, для угла A треугольника ABC

прилежащий катет — это AC.

Соответственно, косинус угла A в треугольнике ABC — это

$\cos \angle A = \frac{{AC}}{{AB}}$

kosinus ugla v treugolnike Для угла B треугольника ABC

прилежащим является катет BC.

Соответственно, косинус угла B в треугольнике ABC

равен отношению BC к AB:

$\cos \angle B = \frac{{BC}}{{AB}}$

Таким образом, косинус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины прилежащего катета на длину гипотенузы.

Длины отрезков — положительные числа, поэтому косинус острого угла прямоугольного треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то косинус острого угла прямоугольного треугольника — число, меньшее единицы.

Вывод:

Косинус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

$0 < \cos \angle A < 1$

Косинус зависит от величины угла.

Если в треугольнике изменить длины сторон, но не изменять угол, значение косинуса этого угла не изменится.

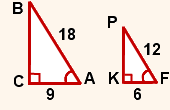
otnoshenie prilezhaschego kateta k gipotenuze

Например,

в треугольниках ABC и FPK

∠A=60º, ∠F=60º.

$\cos \angle A = \frac{{AC}}{{AB}} = \frac{9}{{18}} = \frac{1}{2},$

$\cos \angle F = \frac{{KF}}{{FP}} = \frac{6}{{12}} = \frac{1}{2}.$

Косинус угла в произвольном (не прямоугольном треугольнике) определяется через теорему косинусов. О том, как это делать, мы будем говорить позже.

Косинус острого угла в прямоугольном треугольнике

Добавить комментарий Отменить ответ

Свежие записи

Навигация по сайту

Рубрики