Биссектриса и медиана перпендикулярны |

Задача

В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.

Найти стороны треугольника ABC.

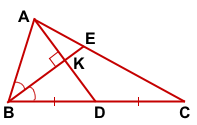bissektrisa-i-mediana-perpendikulyarny Дано: ΔABC,

AD — медиана, BE — биссектриса,

AD=BE=8, AD⊥BE

Найти: AB, BC, AC

Решение:

1) Пусть AD∩BE=K.

Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD. Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

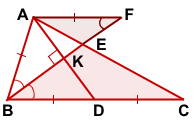
bissektrisa-perpendikulyarna-mediane 3) По свойству биссектрисы треугольника в ΔABC

$\frac{{BC}}{{AB}} = \frac{{CE}}{{AE}} = \frac{2}{1}.$

3) Проведём через точку A прямую, параллельную BC и продлим BE до пересечения с этой прямой в точке F.

Рассмотрим треугольники BEC и FEA.

∠AFB=∠CBF (как внутренние накрест лежащие при BC || AF и секущей BF).

∠BEC=∠FEA (как вертикальные).

Значит треугольники BEC и FEA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac{{BC}}{{FA}} = \frac{{CE}}{{AE}} = \frac{{BE}}{{FE}} = \frac{2}{1}.$

$\frac{{BC}}{{FA}} = \frac{2}{1}, \Rightarrow FA = \frac{1}{2}BC = AB.$

Таким образом, треугольник ABF — равнобедренный с основанием BF, а значит, его высота AK является также медианой и BK=KF.

$\frac{8}{{FE}} = \frac{2}{1}, \Rightarrow FE = 4,$

BF=BE+FE=12, BK=KF=6.

4) Рассмотрим прямоугольный треугольник ABK. По теореме Пифагора

$AB^2 = BK^2 + AK^2 ,$

$AB = \sqrt {6^2 + 4^2 } = \sqrt {52} = 2\sqrt {13} ,$

$BC = 2AB = 4\sqrt {13} .$

5) Рассмотрим прямоугольный треугольник AKE.

KE=BE-BK=8-6=2. По теореме Пифагора

$AE^2 = AK^2 + KE^2 ,$

$AE = \sqrt {4^2 + 2^2 } = \sqrt {20} = 2\sqrt 5 ,$

$\frac{{CE}}{{AE}} = \frac{2}{1}, \Rightarrow CE = 2AE,$

$AC = AE + CE = 3AE = 6\sqrt 5 .$

Ответ:

$2\sqrt {13} ,4\sqrt {13} ,6\sqrt 5 .$

II способ

mediana-i-bissektrisa-perpendikulyarny 1) Пусть AD∩BE=K.

Так как в треугольнике ABD BK — биссектриса и высота, то ΔABC — равнобедренный с основанием AD (по признаку равнобедренного треугольника). Значит, AB=BD.

Следовательно, BC=2AB.

По свойству равнобедренного треугольника BK — медиана и AK=KD=4.

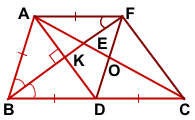
2) Отложим на луче BE с другой стороны от точки K отрезок KF, KF=BK.

Проведём отрезки DF и CF.

Четырёхугольники AFDB и AFCD — параллелограммы (по признаку параллелограмма). Тогда AF=BD, DF=AB, FC=AD (по свойству параллелограмма), а так как AB=BD, то ABCD — ромб.

AC∩DF=O. По свойству параллелограмма O — середина DF. Значит E — точка пересечения медиан треугольника AFD. По свойству медиан FE:EK=2:1. Следовательно

$EK = \frac{1}{3}KF = \frac{1}{3}BK,$