Биссектриса делит гипотенузу |

Биссектриса делит гипотенузу

В каком отношении биссектриса делит гипотенузу?

По свойству биссектрисы треугольника биссектриса делит третью сторону на отрезки, пропорциональные двум другим сторонам.

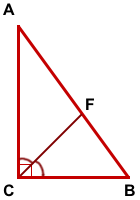bissektrisa-delit-gipotenuzu-na-otrezkiСоответственно, в прямоугольном треугольнике биссектриса делит гипотенузу на отрезки, пропорциональные катетам:

    \[ \frac{{AF}}{{BF}} = \frac{{AC}}{{BC}} \]

либо

    \[ \frac{{AC}}{{AF}} = \frac{{BC}}{{BF}}. \]

Поскольку биссектриса делит площадь треугольника пропорционально прилежащим сторонам, то биссектриса, проведённая к гипотенузе, делит площадь прямоугольного треугольника пропорционально катетам:

    \[ \frac{{S_{\Delta ACF} }}{{S_{\Delta BCF} }} = \frac{{AF}}{{BF}}. \]

Задача.

Биссектриса прямоугольного треугольника делит гипотенузу на отрезки 100 см и 75 см. Найти, на какие части делит гипотенузу высота треугольника.

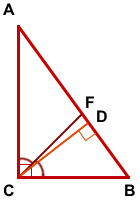bissektrisa-delit-gipotenuzuДано: ΔABC,

CF — биссектриса, AF=100 см, BF=75 см,

CD⊥AB

Найти: AD, BD.

Решение:

По свойству биссектрисы треугольника

    \[ \frac{{AF}}{{BF}} = \frac{{AC}}{{BC}} = \frac{{100}}{{75}} = \frac{4}{3}, \]

откуда

    \[ BC = \frac{3}{4}AC. \]

По теореме Пифагора

    \[AC^2 + BC^2 = AB^2 ,\]

    \[AC^2 + (\frac{3}{4}AC)^2 = AB^2 ,\]

    \[ \frac{{25}}{{16}}AC^2 = AB^2 ,\]

    \[\frac{5}{4}AC = AB\]

(извлечь из обеих частей квадратный корень можем в силу того, что AC>0, AB>0).

AB=AF+BF=175 см. Таким образом,

    \[\frac{5}{4}AC = 175\]

и AC=140 см, BC=105 см.

Высоту, проведённую к гипотенузе, проще всего найти через площадь:

    \[S_{\Delta ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD,\]

следовательно,

    \[CD = \frac{{AC \cdot BC}}{{AB}} = \frac{{140 \cdot 105}}{{175}} = 84cm.\]

Ответ: 84 см.

2 Comments

  1. Требовалось найти одно, нашли другое. Несостыковочка(

    Ответить

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *