Биссектриса CM треугольника ABC |

Биссектриса CM треугольника ABC

Задача

Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=5 и MB=10. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найти CD.

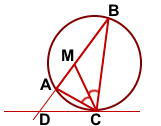bissektrisa-cm-treugolnika-abc Дано: ΔABC вписан в окр.(O;R),

CM — биссектриса ∠ACB, CD — касательная к окр.(O;R),

AM=5, MB=10, CD∩AB=D

Найти: CD

Решение:

1) Рассмотрим треугольник ABC. Так как CM — его биссектриса, то по свойству биссектрисы треугольника

$\frac{{CA}}{{BC}} = \frac{{AM}}{{MB}} = \frac{5}{{10}} = \frac{1}{2}.$

AB=AM+MB=5+10=15. bissektrisa-cm-treugolnika-abc-delit

$2)\angle DCA = \frac{1}{2} \cup AC$

(как угол между касательной и хордой, проведённой в точку касания).

$\angle ABC = \frac{1}{2} \cup AC$

(как вписанный угол, опирающийся на дугу AC).

Следовательно, ∠DCA=∠ABC.

Так как в треугольниках CAD и BCD

∠DCA=∠DBC (по доказанному),
∠D — общий,

то треугольники CAD и BCD подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\frac{{CD}}{{BD}} = \frac{{AD}}{{CD}} = \frac{{CA}}{{BC}} = \frac{1}{2},$

следовательно

$AD = \frac{1}{2}CD,$

и из равенства

$\frac{{CD}}{{BD}} = \frac{{AD}}{{CD}}$

по основному свойству пропорции

$CD^2 = AD \cdot BD.$

Подставим вместо AD 1/2 CD:

$CD^2 = \frac{1}{2}CD \cdot BD,$

делим обе части равенства на CD

$CD = \frac{1}{2}BD.$

Пусть AD=x, тогда BD=AB+AD=15+x, CD=2x.

$2x = \frac{1}{2}(x + 15),$

$4x = x + 15$

$3x = 15$

$x = 5$

CD=2·5=10.

Ответ: 10.

Добавить комментарий Отменить ответ